La méthode Montessori, 2e édition - Restauration # Chapitre 19 - Enseignement de la numération, introduction à l'arithmétique Les enfants de trois ans savent déjà compter jusqu'à deux ou trois lorsqu'ils entrent dans nos écoles. Ils   apprennent  donc ***très facilement la numération, qui consiste à compter des objets** .*  Une douzaine de voies différentes peuvent servir à cette fin, et la vie quotidienne présente de nombreuses opportunités ; quand la mère dit, par exemple, « Il manque deux boutons à ton tablier » ou « Nous avons besoin de trois autres assiettes à table ». Un des premiers moyens que j'utilise est celui de compter avec de l'argent. J'obtiens  de l'argent ***frais***  , et si c'était possible je ferais faire de bonnes reproductions en carton. J'ai vu cet argent utilisé dans une école pour déficients à Londres. La  ***fabrication de monnaie***  est une forme de numération si attrayante qu'elle retient l'attention de l'enfant. Je présente les pièces de un, deux et quatre centimes, et les enfants apprennent ainsi à compter jusqu'à  ***dix** .* Aucun enseignement n'est plus  ***pratique***  que celui qui tend à familiariser les enfants avec les monnaies d'usage courant, et aucun exercice n'est plus utile que celui de rendre la monnaie. Elle est si étroitement liée à la vie quotidienne qu'elle intéresse intensément tous les enfants. Ayant enseigné la numération sur ce mode empirique, je passe à des exercices plus méthodiques, ayant pour matériel didactique un des ensembles de blocs déjà utilisés dans l'éducation des sens ; à savoir, la série de dix tiges utilisées jusqu'ici pour l'enseignement de la longueur. La plus courte de ces tiges correspond à un décimètre, la plus longue à un mètre, tandis que les tiges intermédiaires sont divisées en sections d'un décimètre de longueur. Les sections sont peintes alternativement en rouge et en bleu.  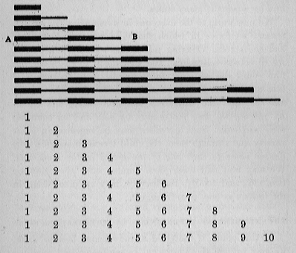Un jour, lorsqu'un enfant a rangé les baguettes en les plaçant par ordre de longueur, on lui fait compter les signes rouges et bleus, en commençant par le plus petit morceau ; c'est-à-dire un ; un deux; un, deux, trois, etc., en remontant toujours à un dans le comptage de chaque réglette, et en partant du côté A. On lui fait alors nommer les réglettes simples de la plus courte à la plus longue, selon le nombre total de sections que chacun contient, touchant les tiges du côté B, de quel côté monte l'escalier. Il en résulte la même numérotation que lorsque l'on comptait la tige la plus longue 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Souhaitant connaître le nombre de tiges, on les compte du côté A et de même résultats de numération ; 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Nous unissons maintenant les exercices de  ***numération***  aux exercices sensoriels antérieurs dans lesquels l'enfant reconnaissait les tiges longues et courtes. Après avoir mélangé les baguettes sur un tapis, la directrice en choisit une, et la montrant à l'enfant, lui fait compter les sections ; par exemple, 5. Elle lui demande alors de lui donner la longueur suivante. Il la sélectionne à l'  ***œil*** , et la directrice lui fait  ***vérifier***  son choix en  ***plaçant les deux pièces côte à côte et en comptant leurs sections** .*  De tels exercices peuvent être répétés dans une grande variété et à travers eux, l'enfant apprend à attribuer un  ***nom particulier à chacune des pièces du long escalier** .* Nous pouvons maintenant les appeler pièce numéro un ; morceau numéro deux, etc., et enfin, par souci de brièveté, peut en parler dans les leçons comme un, deux, trois, etc. ## [19.1 Numéros représentés par des signes graphiques](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+19+-+Teaching+of+numeration%3A+Introduction+to+arithmetic#19.1-numbers-as-represented-by-graphic-signs 'Lien vers le texte de base de traduction de Montessori.Zone "La méthode Montessori"') A ce stade, si l'enfant sait déjà écrire, on peut présenter les figures découpées dans du papier de verre et montées sur des cartes. En les présentant, la méthode est la même que celle utilisée pour enseigner les lettres. "C'est un." "C'est deux." "Donne m'en un." "Donnez-m'en deux." "Quel  *numéro*  est-ce?" L'enfant trace le chiffre avec son doigt comme il trace les lettres. ***Exercices avec des nombres** .*  Association du signe graphique à la quantité. J'ai conçu deux plateaux divisés chacun en cinq petits compartiments. Au fond de chaque compartiment peut être placée une carte portant un chiffre. Les chiffres du premier plateau doivent être 0, 1, 2, 3, 4 et dans le second, 5, 6, 7, 8 et 9. L'exercice est évident ; il consiste à placer dans les compartiments des objets correspondant au chiffre indiqué sur la carte au fond du compartiment. Nous donnons aux enfants divers objets pour varier la leçon, mais nous utilisons surtout de grosses chevilles en bois taillées de telle sorte qu'elles ne roulent pas du pupitre. On en place un certain nombre devant l'enfant chargé de les ranger à leur place, une cheville correspondant à la carte marquée un, etc. Quand il a fini, il apporte son plateau à la directrice pour qu'elle vérifie son travail. ***La leçon sur zéro** .*  Nous attendons que l'enfant, désignant le compartiment contenant la carte marquée zéro, demande : "Et qu'est-ce que je dois mettre ici ?" Nous répondons alors, "Rien; zéro n'est rien." Mais souvent cela ne suffit pas. Il faut faire  ***ressentir*** à l'enfant  ce que l'on entend par  ***rien** .*  Pour cela, nous utilisons des petits jeux qui amusent énormément les enfants. Je me tiens parmi eux, et en me tournant vers l'un d'entre eux qui a déjà utilisé ce matériel, je dis : « Viens, ma chérie, viens me voir  ***zéro***  fois. L'enfant vient presque toujours vers moi, puis revient en courant chez lui. "Mais, mon garçon, tu es venu  ***une***  fois, et je t'ai dit de venir  ***zéro*** fois." Alors il commence à se demander. "Mais que dois-je faire, alors?" "Rien; zéro c'est rien." "Mais comment est-ce que je ne ferai rien ?" "Ne fais rien. Vous devez rester assis. Vous ne devez pas venir du tout, pas n'importe quand. Zéro fois. Pas de temps du tout. » Je répète ces exercices jusqu'à ce que les enfants comprennent, et ils s'amusent alors immensément à rester silencieux quand je leur crie de venir vers moi zéro fois ou de me jeter zéro bisous. Ils crient souvent : « Zéro c'est rien! Zéro c'est rien !" ## [19.2 Exercices pour la mémoire des nombres](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+19+-+Teaching+of+numeration%3A+Introduction+to+arithmetic#19.2-exercises-for-the-memory-of-numbers 'Lien vers le texte de base de traduction de Montessori.Zone "La méthode Montessori"') Lorsque les enfants reconnaissent le chiffre écrit, et que ce chiffre leur signifie la valeur numérique, je leur donne l'exercice suivant : Je découpe les chiffres de vieux calendriers et les monte sur des bouts de papier qui sont ensuite pliés et déposés dans une boîte. Les enfants tirent les feuillets et les portent encore pliés, jusqu'à leurs sièges, où ils les regardent et les replient en  ***gardant le secret** .*  Puis, un par un, ou par groupes, ces enfants (qui sont naturellement les plus âgés de la classe) se dirigent vers la grande table de la directrice où ont été disposés des groupes de petits objets divers. Chacun sélectionne la  ***quantité***  d'objets correspondant au nombre qu'il a tiré. Le numéro, quant à lui, a été déposé  ***chez l'enfant*** , un bout de papier mystérieusement plié. L'enfant doit donc  ***se rappeler*** son numéro non seulement pendant les mouvements qu'il fait en allant et venant mais pendant qu'il ramasse ses pièces, en les comptant une à une. La directrice peut ici faire des observations individuelles intéressantes sur la mémoire des nombres. Quand l'enfant a ramassé ses objets, il les dispose sur sa propre table, en colonnes de deux, et si le nombre est impair, il place la pièce impaire en bas et entre les deux derniers objets. La disposition des pièces est donc la suivante : ``` o o o o o o o o o o X XX XX XX XX XX XX XX XX XX X XX XX XX XX XX XX XX X XX XX XX XX XX X XX XX XX X XX ``` Les croix représentent les objets, tandis que le cercle représente le bordereau plié contenant la figure. Après avoir rangé ses objets, l'enfant attend la vérification. La directrice vient, ouvre le bordereau, lit le numéro et compte les pièces. Lorsque nous avons joué pour la première fois à ce jeu, il arrivait souvent que les enfants prenaient  ***plus d'objets***  qu'il n'était demandé sur la carte, et ce n'était pas toujours parce qu'ils ne se souvenaient pas du nombre, mais c'était la manie d'avoir le plus grand nombre d'objets. Un peu de cette gourmandise instinctive, qui est commune à l'homme primitif et inculte. La directrice cherche à expliquer aux enfants qu'il est inutile d'avoir toutes ces choses sur le bureau et que le but du jeu est de prendre le nombre exact d'objets demandés. Peu à peu, ils entrent dans cette idée, mais pas aussi facilement qu'on pourrait le croire. C'est un véritable effort d'abnégation qui maintient l'enfant dans la limite fixée et lui fait prendre, par exemple, seulement deux des objets mis à sa disposition, alors qu'il voit les autres en prendre davantage. Je considère donc ce jeu plus comme un exercice de volonté que de numération. L'enfant qui a le  ***zéro*** , ne doit pas bouger de sa place lorsqu'il voit tous ses compagnons se lever et prendre librement des objets qui lui sont inaccessibles. Plusieurs fois zéro tombe sur le sort d'un enfant qui sait parfaitement compter, et qui éprouverait un grand plaisir à accumuler et disposer sur sa table un beau groupe d'objets dans le bon ordre, et à attendre avec sécurité la vérification du maître. Il est très intéressant d'étudier les expressions sur les visages de ceux qui possèdent le zéro. Les différences individuelles qui en résultent sont presque un révélateur du "caractère" de chacun. Certains restent impassibles, assumant un front audacieux pour cacher la douleur de la déception ; d'autres manifestent cette déception par des gestes involontaires. Pourtant, d'autres ne peuvent cacher le sourire que suscite la situation singulière dans laquelle ils se trouvent et qui rendra curieux leurs amis. Il y a des petits qui suivent chaque mouvement de leurs compagnons avec un regard de désir, presque d'envie, tandis que d'autres montrent une acceptation instantanée de la situation. Non moins intéressantes sont les expressions avec lesquelles ils avouent détenir le zéro lorsqu'on leur demande lors de la vérification, « et toi, tu n'as rien pris ? "J'ai zéro." "C'est zéro." Ce sont les mots habituels, mais le visage expressif et le ton de la voix montrent des sentiments très variés. Rares, en effet, ceux qui semblent donner avec plaisir l'explication d'un fait extraordinaire. Le plus grand nombre a l'air mécontent ou simplement résigné. Nous donnons donc des leçons sur le sens du jeu, en disant : « Il est difficile de ne garder aucun secret. Pliez bien le papier et ne le laissez pas s'échapper. C'est le plus difficile de tous. En effet, au bout d'un moment, c'est la difficulté même de se taire qui séduit les enfants, et lorsqu'ils ouvrent le bulletin marqué zéro, on constate qu'ils se contentent de garder le secret. ## [19.3 Addition et soustraction de un à vingt : multiplication et division](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+19+-+Teaching+of+numeration%3A+Introduction+to+arithmetic#19.3-addition-and-subtraction-from-one-to-twenty%3A-multiplication-and-division 'Lien vers le texte de base de traduction de Montessori.Zone "La méthode Montessori"') Le matériel didactique que nous utilisons pour l'enseignement des premières opérations arithmétiques est le même déjà utilisé pour la numération ; c'est-à-dire les réglettes graduées en longueur qui, disposées sur l'échelle du mètre, contiennent la première idée du système décimal. Les baguettes, comme je l'ai dit, sont appelées par les nombres qu'elles représentent ; un, deux, trois, etc. Ils sont rangés par ordre de longueur, qui est aussi par ordre de numération. Le premier exercice consiste à essayer d'assembler les morceaux les plus courts de manière à former des dizaines. La façon la plus simple de le faire est de prendre successivement les réglettes les plus courtes, de une en haut, et de les placer au bout des longues réglettes correspondantes en commençant par neuf. Cela peut être accompagné des commandes suivantes : "Prenez un et ajoutez-le à neuf ; prenez deux et ajoutez-le à huit ; prenez trois et ajoutez-le à sept ; prenez quatre et ajoutez-le à six." De cette façon, nous faisons quatre tiges égales à dix. Reste le cinq, mais, le renversant (au sens long), il passe d'un bout à l'autre du dix, et met ainsi en évidence le fait que deux fois cinq font dix. Ces exercices sont répétés et peu à peu l'enfant apprend le langage le plus technique ; neuf plus un égal dix, huit plus deux égal dix, sept plus trois égal dix, six plus quatre égal dix, et pour le cinq qui reste, deux fois cinq égal dix. Enfin, s'il sait écrire, nous enseignons les signes  *plus*  et  *égal*  et  les *temps.*  Alors voici ce que nous voyons dans les carnets soignés de nos petits : ``` 9+1=10 8+2=10 5x2=10 7+3=10 6+4=10 ``` Quand tout cela est bien appris et mis sur le papier avec grand plaisir par les enfants, nous attirons leur attention sur le travail qui s'effectue lorsque les pièces groupées en dizaines sont démontées et remises dans leur position d'origine. Des dix derniers formés, nous retirons quatre et six restes; du suivant, nous retirons trois et sept restes; du suivant, deux et huit restes; du dernier, nous enlevons un et neuf restes. En parlant de cela proprement, nous disons : dix moins quatre égalent six ; dix moins trois égale sept ; dix moins deux égale huit ; dix moins un égale neuf. Quant aux cinq restants, c'est la moitié de dix, et en coupant la longue tige en deux, c'est-à-dire en divisant dix par deux, nous aurions cinq; dix divisé par deux égale cinq. La trace écrite de tout cela se lit comme suit : ``` 10-4=6 10-3=7 10 / 2=5 10-2=8 10-1=9 ``` Une fois que les enfants ont maîtrisé cet exercice, ils le multiplient spontanément. Peut-on en faire trois de deux manières ? Nous plaçons le un après les deux et écrivons ensuite, pour nous souvenir de ce que nous avons fait, 2+1=3. Pouvons-nous faire deux réglettes égales au nombre quatre ? 3+1=4 et 4-3=1 ; 4-1=3. La tige numéro deux dans sa relation avec la tige numéro quatre est traitée comme était cinq par rapport à dix ; c'est-à-dire que nous la retournons et montrons qu'elle est contenue dans quatre exactement deux fois : 4/2=2 ; 2x2=4. Autre problème : voyons avec combien de baguettes on peut jouer à ce même jeu. Nous pouvons le faire avec trois et six, et avec quatre et huit ; C'est, ``` 2x2=4 3x2=6 4x2=8 5x2=10 10/2=5 8/2=4 6/2=3 4/2=2 ``` À ce stade, nous constatons que les cubes avec lesquels nous avons joué aux jeux de mémoire de nombres sont utiles :  De cette disposition, on voit tout de suite quels sont les nombres divisibles par deux de tous ceux qui n'ont pas de cube impair au fond. Ce sont les  nombres ***pairs***  car ils peuvent être disposés par paires, deux par deux ; et la division par deux est facile, il suffit de séparer les deux lignes de deux qui se tiennent l'une sous l'autre. En comptant les cubes de chaque fichier, nous avons le quotient. Pour recomposer le nombre primitif il suffit de réassembler les deux fichiers donc 2x3=6. Tout cela n'est pas difficile pour des enfants de cinq ans. La répétition devient bientôt monotone, mais les exercices peuvent être plus facilement changés, en reprenant l'ensemble des longues réglettes, et au lieu de placer la réglette numéro une après neuf, placez-la après dix. De la même manière, placez deux après neuf et trois après huit. De cette manière, nous fabriquons des tiges d'une longueur supérieure à dix; longueurs qu'il faut apprendre à nommer onze, douze, treize, etc., jusqu'à vingt. Les petits cubes aussi peuvent être utilisés pour fixer ces nombres plus élevés Après avoir appris les opérations par dix, nous passons sans difficulté à vingt. La seule difficulté réside dans les  ***nombres décimaux***  qui nécessitent certaines leçons. ## [19.4 Leçons sur les nombres décimaux : calculs arithmétiques au-delà de dix](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+19+-+Teaching+of+numeration%3A+Introduction+to+arithmetic#19.4-lessons-on-decimals%3A-arithmetical-calculations-beyond-ten 'Lien vers le texte de base de traduction de Montessori.Zone "La méthode Montessori"') Le matériel didactique nécessaire se compose d'un certain nombre de cartes carrées sur lesquelles le chiffre dix est imprimé en gros caractères, et d'autres cartes rectangulaires, la moitié de la taille du carré, et contenant les chiffres simples de un à neuf. Nous plaçons les nombres sur une ligne; 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Puis, n'ayant plus de chiffres, il faut recommencer et reprendre le 1. Ce 1 est comme cette section dans le jeu de tiges qui, dans la tige numéro 10, s'étend au-delà de neuf. Compter le long  ***de l'escalier*** jusqu'à neuf, il reste cette seule section que, comme il n'y a plus de nombres, nous désignons à nouveau par 1; mais c'est un 1 plus élevé que le premier, et pour le distinguer du premier on met près de lui un zéro, signe qui ne veut rien dire. Voici donc 10. Couvrant le zéro avec les cartes numérotées rectangulaires séparées dans l'ordre de leur succession, nous voyons formé : 11, 12, 13, 14, 15, 16, 17, 18, 19. Ces nombres sont composés en ajoutant à la tige numéro 10, première réglette numéro 1, puis 2, puis 3, etc., jusqu'à ce qu'on ajoute finalement la réglette numéro 9 à la réglette numéro 10, obtenant ainsi une réglette très longue, qui, lorsqu'elle alterne les sections rouges et bleues sont comptées, donne nous dix-neuf.  La directrice peut alors montrer à l'enfant les cartes, en donnant le nombre 16, et il peut placer la tige 6 après la tige 10. Elle enlève alors la carte portant le 6, et place sur le zéro la carte portant le chiffre 8, sur quoi l'enfant enlève la tige 6 et la remplace par la tige 8, faisant ainsi 18. Chacun de ces actes peut être noté ainsi : 10+6=16 ; 10+8=18, etc. On procède de la même manière à la soustraction. 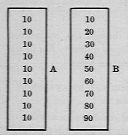Lorsque le nombre lui-même commence à avoir une signification claire pour l'enfant, les combinaisons sont faites sur une longue carte, en disposant les cartes rectangulaires portant les neuf chiffres sur les deux colonnes de nombres indiquées dans les figures A et B. Sur la carte A, nous superposons au zéro du deuxième 10, la carte rectangulaire portant le 1 : et en dessous celle portant le deux, etc. Ainsi, tant que l'un des dix reste le même, les nombres de droite vont de zéro à neuf, Donc:  Dans la carte B, les applications sont plus complexes. Les cartes sont superposées en progression numérique par dizaines. Presque tous nos enfants comptent jusqu'à 100, un nombre qui leur a été donné en réponse à la curiosité qu'ils manifestaient pour l'apprendre. Je ne crois pas que cette phase de l'enseignement ait besoin d'autres illustrations. Chaque enseignant peut multiplier les exercices pratiques dans les opérations arithmétiques, en utilisant des objets simples que les enfants peuvent facilement manipuler et diviser. > ##### **La licence de cette page :** > > Cette page fait partie du « **Projet de restauration et de traduction Montessori** ».\ > Veuillez [soutenir](https://ko-fi.com/montessori) notre initiative " **Éducation Montessori tout compris pour tous 0-100+ dans le monde** ". Nous créons des ressources ouvertes, gratuites et abordables disponibles pour tous ceux qui s'intéressent à l'éducation Montessori. Nous transformons les personnes et les environnements pour qu'ils soient authentiques Montessori dans le monde entier. Merci! > > [](http://creativecommons.org/licenses/by-nc-sa/4.0/) > > **Licence :** Ce travail avec toutes ses modifications de restauration et traductions est sous licence  [Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License](http://creativecommons.org/licenses/by-nc-sa/4.0/) . > > Consultez l' **historique** des pages de chaque page wiki dans la colonne de droite pour en savoir plus sur tous les contributeurs et les modifications, restaurations et traductions effectuées sur cette page. > > [Les contributions](https://ko-fi.com/montessori) et les [sponsors](https://ko-fi.com/montessori) sont les bienvenus et très appréciés ! * [La méthode Montessori, 2e édition](https://montessori-international.com/s/the-montessori-method/wiki/French "La méthode Montessori sur la zone Montessori - Langue anglaise") - Restauration en français - [Archive.Org](https://archive.org/details/montessorimethod00montuoft/ "La méthode Montessori sur Aechive.Org") - [Open Library](https://openlibrary.org/books/OL7089223M/The_Montessori_method "La méthode Montessori sur la bibliothèque ouverte") * [0 - Index des chapitres - La méthode Montessori, 2e édition - Restauration - Bibliothèque ouverte](https://montessori-international.com/s/the-montessori-method/wiki/0+-+Index+des+chapitres+-+La+m%C3%A9thode+Montessori%2C+2e+%C3%A9dition+-+Restauration+-+Biblioth%C3%A8que+ouverte) * [Chapitre 00 - Dédicace, remerciements, préface à l'édition américaine, introduction](https://montessori-international.com/s/the-montessori-method/wiki/Chapitre+00+-+D%C3%A9dicace%2C+remerciements%2C+pr%C3%A9face+%C3%A0+l%27%C3%A9dition+am%C3%A9ricaine%2C+introduction) * [Chapitre 01 - Une réflexion critique sur la nouvelle pédagogie dans son rapport à la science moderne](https://montessori-international.com/s/the-montessori-method/wiki/Chapitre+01+-+Une+r%C3%A9flexion+critique+sur+la+nouvelle+p%C3%A9dagogie+dans+son+rapport+%C3%A0+la+science+moderne) * [Chapitre 02 - Histoire des méthodes](https://montessori-international.com/s/the-montessori-method/wiki/Chapitre+02+-+Histoire+des+m%C3%A9thodes) * [Chapitre 03 - Discours inaugural prononcé à l'occasion de l'ouverture d'une des « Maisons des Enfants »](https://montessori-international.com/s/the-montessori-method/wiki/Chapitre+03+-+Discours+inaugural+prononc%C3%A9+%C3%A0+l%27occasion+de+l%27ouverture+d%27une+des+%C2%AB+Maisons+des+Enfants+%C2%BB) * [Chapitre 04 - Méthodes pédagogiques utilisées dans les « Maisons des enfants »](https://montessori-international.com/s/the-montessori-method/wiki/Chapitre+04+-+M%C3%A9thodes+p%C3%A9dagogiques+utilis%C3%A9es+dans+les+%C2%AB+Maisons+des+enfants+%C2%BB) * [Chapitre 05 - Discipline](https://montessori-international.com/s/the-montessori-method/wiki/Chapitre+05+-+Discipline) * [Chapitre 06 - Comment la leçon doit être donnée](https://montessori-international.com/s/the-montessori-method/wiki/Chapitre+06+-+Comment+la+le%C3%A7on+doit+%C3%AAtre+donn%C3%A9e) * [Chapitre 07 - Exercices pour la vie pratique](https://montessori-international.com/s/the-montessori-method/wiki/Chapitre+07+-+Exercices+pour+la+vie+pratique) * [Chapitre 08 - Réflexion sur l'alimentation de l'enfant](https://montessori-international.com/s/the-montessori-method/wiki/Chapitre+08+-+R%C3%A9flexion+sur+l%27alimentation+de+l%27enfant) * [Chapitre 09 - Gymnastique d'éducation musculaire](https://montessori-international.com/s/the-montessori-method/wiki/Chapitre+09+-+Gymnastique+d%27%C3%A9ducation+musculaire) * [Chapitre 10 - La nature dans l'enseignement du travail agricole : Culture des plantes et des animaux](https://montessori-international.com/s/the-montessori-method/wiki/Chapitre+10+-+La+nature+dans+l%27enseignement+du+travail+agricole+%3A+Culture+des+plantes+et+des+animaux) * [Chapitre 11 - Le travail manuel l'art du potier, et la construction](https://montessori-international.com/s/the-montessori-method/wiki/Chapitre+11+-+Le+travail+manuel+l%27art+du+potier%2C+et+la+construction) * [Chapitre 12 - L'éducation des sens](https://montessori-international.com/s/the-montessori-method/wiki/Chapitre+12+-+L%27%C3%A9ducation+des+sens) * [Chapitre 13 - Education des sens et illustrations du matériel didactique : Sensibilité générale : Les sens tactiles, thermiques, basiques et stéréognostiques](https://montessori-international.com/s/the-montessori-method/wiki/Chapitre+13+-+Education+des+sens+et+illustrations+du+mat%C3%A9riel+didactique+%3A+Sensibilit%C3%A9+g%C3%A9n%C3%A9rale+%3A+Les+sens+tactiles%2C+thermiques%2C+basiques+et+st%C3%A9r%C3%A9ognostiques) * [Chapitre 14 - Notes générales sur l'éducation des sens](https://montessori-international.com/s/the-montessori-method/wiki/Chapitre+14+-+Notes+g%C3%A9n%C3%A9rales+sur+l%27%C3%A9ducation+des+sens) * [Chapitre 15 - Education intellectuelle](https://montessori-international.com/s/the-montessori-method/wiki/Chapitre+15+-+Education+intellectuelle) * [Chapitre 16 - Méthode d'enseignement de la lecture et de l'écriture](https://montessori-international.com/s/the-montessori-method/wiki/Chapitre+16+-+M%C3%A9thode+d%27enseignement+de+la+lecture+et+de+l%27%C3%A9criture) * [Chapitre 17 - Description de la méthode et du matériel didactique utilisé](https://montessori-international.com/s/the-montessori-method/wiki/Chapitre+17+-+Description+de+la+m%C3%A9thode+et+du+mat%C3%A9riel+didactique+utilis%C3%A9) * [Chapitre 18 - Le langage dans l'enfance](https://montessori-international.com/s/the-montessori-method/wiki/Chapitre+18+-+Le+langage+dans+l%27enfance) * [Chapitre 19 - Enseignement de la numération : Introduction à l'arithmétique](https://montessori-international.com/s/the-montessori-method/wiki/Chapitre+19+-+Enseignement+de+la+num%C3%A9ration+%3A+Introduction+%C3%A0+l%27arithm%C3%A9tique) * [Chapitre 20 - Séquence d'exercice](https://montessori-international.com/s/the-montessori-method/wiki/Chapitre+20+-+S%C3%A9quence+d%27exercice) * [Chapitre 21 - Révision générale de la discipline](https://montessori-international.com/s/the-montessori-method/wiki/Chapitre+21+-+R%C3%A9vision+g%C3%A9n%C3%A9rale+de+la+discipline) * [Chapitre 22 - Conclusions et impressions](https://montessori-international.com/s/the-montessori-method/wiki/Chapitre+22+-+Conclusions+et+impressions) * [Chapitre 23 - Illustrations](https://montessori-international.com/s/the-montessori-method/wiki/Chapitre+23+-+Illustrations)